Programação não Linear (volume)

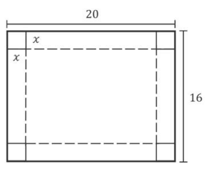
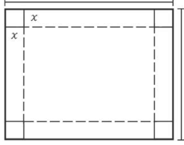
        Tomaremos como exemplo uma folha de papel retangular com lados 20 cm e 16 cm. Após remover um quadrado de lado x cm de cada um dos cantos da folha, foram feitas 4 dobras para construir uma caixa (sem tampa) em forma de paralelepípedo reto-retângulo com altura x cm. As linhas tracejadas na figura indicam onde as dobras foram feitas.

Folha de papel (figura 01)

Caixa após as dobras (figura 02)

         Qual a medida X a ser cortada para a caixa ter o maior volume possível?

        Volume = comprimento * largura * altura ==> V = C * L * A
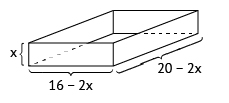
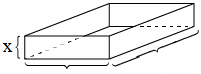
         Conforme mostra na figura 02 ,
        comprimento (C) = 20 – 2X
        largura (L) = 16 – 2X
        altura (A) = X
        Portanto, o volume V = (20 – 2X) * ( 16 – 2X) * X
        Aplicando a distributiva, temos :
V = (20 * 16 * X) + (20 * - 2X * X) + (- 2X * 16 * X) + (- 2X * - 2X * X )
V = 320 X - 40 X² - 32 X² + 4 X³
V = 320 X – 72 X² + 4 X³ ;
ordenando pelo expoente,
V = 4 X³ – 72 X² + 320 X ;
derivando, temos:
12 X² - 144 X + 320 = 0
Utilizando Bhaskara, temos 2 raízes
X1 = 9,06     e     X2 = 2,94

         Conclusão : O valor de X é 2,94 , pois, se usarmos 9,06 , para calcular a largura L = 16 – 2 X, teríamos uma medida negativa.

APLICAÇÃO

Digite o comprimento:
Digite a largura:                           





                                    




    
    
    
    
    
    
    
                    


      ± √   
              
                                          

                ± √      
                ± √  
                ±
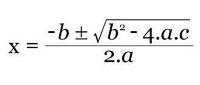