CONTATO:
 (11)97422-0547
(11)97422-0547
 seba@sebacampos.com.br
seba@sebacampos.com.br
 (11)3230-6164
(11)3230-6164
 henrique@obispo.com.br
henrique@obispo.com.br
 (11)97422-0547
(11)97422-0547
 seba@sebacampos.com.br
seba@sebacampos.com.br
 (11)3230-6164
(11)3230-6164
 henrique@obispo.com.br
henrique@obispo.com.br
O que é Custo de Armazenagem?
Custos de armazenagem representam os custos da área física ocupada pelo armazém, despesas de manutenção, equipamentos, mão de obra, administrativas, seguros, prejuízos diversos ocorridos na atividade de armazenagem (quebras, perdas, roubos). Enfim, todas despesas do setor de armazenagem.Para calcular o custo de armazenagem (CA), utilizamos a seguinte fórmula:
onde, EM é o estoque médio no período, Pmu é o preço médio unitário ou valor médio, t é o tempo ou período, Cau é o custo de armazenagem unitário (fator)
Etapas para o Custeio da ArmazenagemEM = ∑ estoques finais / t
Como calcular o preço médio do
produto
O preço ou valor médio do produto é
calculado
dividindo o valor total dos estoques no periodo
pelo total dos estoques no periodo
Pmu = ∑ valores dos estoques / ∑ estoques
finais
Como calcular o custo de armazenagem
unitário
O custo de Armazenagem unitario é
calculado
dividindo o total das despesas pelo
valor médio do estoque
Usamos algumas despesas pré selecionadas, tais como: Aluguel(A),
juros(J), seguro(S),
impostos(I),
perdas(P), movimentação(MV),
mão de
obra(MO) e despesas gerais(D)
Cau = (A + J + S + I + P + MV + MO + D) / VME
Usaremos o método da média simples para a movimentação:
Preencha os campos na tabela abaixo
| Mês | Est. Inic. | Entradas | P.Unit. | Saídas | Est.Final | V.Estoq. |
|---|---|---|---|---|---|---|
| 01 | ||||||
| 02 | ||||||
| 03 | ||||||
| 04 | ||||||
| 05 | ||||||
| 06 | ||||||
| 07 | ||||||
| 08 | ||||||
| 09 | ||||||
| 10 | ||||||
| 11 | ||||||
| 12 | ||||||
| Tot. (∑) dos estoq. = | Valor tot. (∑) dos estoq. = | |||||
| Estoq. médio = | Preço médio($) = | |||||
| Lançar despesas | ||||||
| Desp.Aluguel: | Desp.Juros: | Desp.Seguro: | ||||
| Desp.Impostos: | Desp.Perdas: | Desp.Movim.: | ||||
| Desp.M. obra.: | Desp.Gerais.: | |||||
| Tot. Desp.($)= | V.M.E.($) | Cau= | ||||
A analise dos estoques baseia-se na previsão do consumo do material – onde, a previsão de vendas define as estimativas futuras dos produtos que a empresa produzirá. Estabelecendo assim, quais produtos, quantos produtos e quando serão adquiridos pelos consumidores.
Calcular o ponto de pedido dos produtos usados na sua empresa é uma conduta preventiva.Essa atitude ajuda a estar sempre preparado para imprevistos na demanda dos seus serviços. Afinal, o seu negócio terá um estoque mínimo para garantir o funcionamento do trabalho nesses momentos de alteração na procura.
O ponto de pedido é o momento certo para fazer uma nova compra de estoque, com o intuito de repor algum produto usado na sua empresa. Alguns conceitos são vitais para um bom entendimento sobre o dimensionamento de estoque, são eles:
O consumo médio CM , é a média aritmética do consumo previsto ou realizado num determinado período.
O tempo de reposição TR, também conhecido como Lead Time ou prazo de entrega, é o tempo necessário desde a verificação de que o estoque deve ser reposto até a chegada efetiva da mercadoria na empresa.
Estoque de Segurança ES – é a quantidade de material destinada a evitar ruptura de estoque, ocasionada por dilatação de tempo de ressuprimento (atrasos na entrega ou qualidade) ou aumento de demanda em relação ao previsto.
Existem varias maneiras de calcular o ES. Usaremos a seguinte fórmula : ES = CM * TR , ou seja, a empresa deve ter no mínimo material ate que o novo pedido seja entregue.
Cada empresa adota o estoque de segurança que lhe convém, algumas trabalham com estoque de segurança igual a zero.
Pode-se usar, por exemplo, estoque de segurança para 15 dias ou 30 dias
Ponto de pedido ou ponto de encomenda PP, informa quando é necessário suprir determinado item de estoque, tomando como base o consumo médio.
Se usarmos o TR em dias o CM será o consumo médio diário, se o TR for em mês, o CM será o consumo médio mensal e assim por diante
Lote econômico de compra (LEC), refere à quantidade de material que se compra ou que a empresa produz de cada vez.. Definir o tamanho do lote de compra é importante porque viabiliza a redução dos custos de estocagem
Segundo CORRÊA, o LEC (lote econômico de compra) também denominado EOQ (economical order quantity) gira em torno de um ponto ideal, onde a compra será mais econômica para a empresa. De acordo com o autor, esse ponto, é o que possui menor custo total quando ocorre uma equivalência entre o custo do pedido e o custo de posse. O lote econômico visa determinar o número ideal de pedidos a serem feitos e a quantidade ideal de cada lote.
Para calcular o lote economico de compra, usaremos a seguinte fórmula
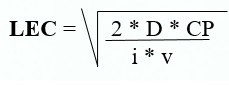
Onde,
D é a demanda,
ou seja, o consumo médio do produto no periodo
CP é a custo para emissão de um pedido.
i são os juros, ou o custo financeiro(%)
V é o valor unitário do produto.
A unidade da demanda, pode ser em peças, quilos, litros, metros,etc. A unidade do custo de pedido (CP) é unidade monetária($); a unidade de juros em em %, porem, na formula devera ser em fator, por ex.; 10% sera 0,10 e assim por diante. O valor(V) também é unidade monetária($)
Os juros e a demanda, deverão estar sempre na mesma unidade de tempo, por exemplo, se os juros forem anual, a demanda tambem será anual; se forem mensal, a demanda tambem será mensal.
Freqüência de pedidos(FEP): é a quantidade de pedidos que deverão ser feitos para atender a demanda. O FEP é sempre arredondado para cima e é calculado pela fórmula:
Tempo entre pedidos(TEP): período, em dias entre os pedidos emitidos. O TEP é calculado pela fórmula:
O 360 corresponde ao ano contabil que é 360 dias
Custo total economico (CTE): .O CTE é calculado pela fórmula:
Lote econômico de fabricação (LEF), refere à quantidade de produto que se produz levando em consideração o custo da preparação da maquina ou da linha de produção, a demanda do produto, o custo de fabricação, a capacidade de produção, os dias ou horas trabalhadas e os juros.
Para calcular o lote economico de fabricação, usaremos a seguinte fórmula
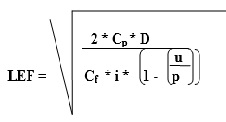
Onde,
D é a demanda,
ou seja, o consumo médio do produto no periodo
CP é a custo de preparação da maquina ou da linha de produção.
CF é a custo unitario de fabricação.
i são os juros, ou o custo financeiro(%)
P é a capacidade de produção, ou seja a produção máxima por dia ou por hora
U é a utilização para produzir. Por ex.: numero total de dias ou de horas que a empresa utiliza
A unidade da demanda, pode ser em peças, quilos, litros, metros, etc. A unidade do custo de preparação (CP) é unidade monetária($); a unidade de juros em em %, porem, na formula devera ser em fator, por ex.; 10% será 0,10 e assim por diante. Porem, deve-se digitar a porcentagem que o sistema faz a transformação em decimais. O custo de fabricação(CF) também é unidade monetária($), a capacidade de produção(P) é dada em peças/hora; peças/dia; etc
A taxa de utilização a unidade pode ser em dias, horas, minutos e assim por diante
Para melhor compreençao, vamos adotar os seguintes critérios:
Quando a demanda for anual, usaremos a taxa de utilização(U), em dias e a capacidade de produção (P), produção diária.
Quando a demanda for mensal, usaremos a taxa de utilização(U), em horas e a capacidade de produção (P), produção horária.
s juros e a demanda, deverão estar sempre na mesma unidade de tempo, por exemplo, se os juros forem anual, a demanda tambem será anual; se forem mensal, a demanda tambem será mensal.
Número de lotes (N), é a quantidade de lotes que deverão ser feitos para atender a demanda. È calculado peça formula:
Custo do sistema CTE ou CS = custo de fabricação + custo para preparar a produção + custo para manter o estoque. É calculado pela fórmula:
O estoque médio(Emédio) é clculado pela formula:
O que é Reta dos mínimos quadrados?
O Método dos Mínimos Quadrados
(MMQ), ou Mínimos Quadrados Ordinários (MQO) ou OLS (do inglês Ordinary Least Squares) é uma
técnica de otimização matemática que procura encontrar o melhor ajuste para um conjunto de dados
tentando minimizar a soma dos quadrados das diferenças entre o valor estimado e os dados
observados (tais diferenças são chamadas resíduos).
É a forma de estimação mais amplamente utilizada na
econometria. Consiste em um estimador que minimiza a soma dos quadrados dos resíduos da
regressão, de forma a maximizar o grau de ajuste do modelo aos dados observados.
Um requisito para o método dos mínimos quadrados é que o fator imprevisível (erro) seja
distribuído aleatoriamente e essa distribuição seja normal.
O Teorema Gauss-Markov garante (embora indiretamente)
que o estimador de mínimos quadrados é o estimador não-enviesado de mínima variância linear na
variável resposta.
Outro requisito é que o modelo é linear nos
parâmetros, ou seja, as variáveis apresentam uma relação linear entre si. Caso contrário,
deveria ser usado um modelo de regressão não-linear.
Credita-se Carl Friedrich Gauss como o desenvolvedor
das bases fundamentais do método dos mínimos quadrados, em 1795, quando Gauss tinha apenas
dezoito anos. Entretanto, Adrien-Marie Legendre foi o primeiro a publicar o método em 1805, em
seu Nouvelles méthodes pour la détermination des orbites des comètes. Gauss publicou suas
conclusões apenas em 1809.
A nossa aplicaçao será utlizada para calcular demandas futuras
Em todos estes problemas, o objetivo do ajuste é obter os valores numéricos de parâmetros cujo significado é definido pelo modelo teórico que está sendo ajustado.
Os dados experimentais são tratados de modo que os valores numéricos obtidos possam ser ajustados a uma reta, cuja equação geral tem a forma y = a + bx ,onde a é o ponto em que a reta intercepta o eixo y e b é a inclinação da reta, definida como b = Δy/Δx.
Todos estes problemas reduzem-se portanto ao ajuste de uma reta a um conjunto de pontos obtidos a partir de dados experimentais.
Exemplo
Considere, por exemplo, o conjunto de pares ordenados (x,y) apresentados na Tabela abaixo que foram obtidos como resultados de medidas da propriedade y correspondentes a diferentes valores da propriedade x.

Os pares ordenados da Tabela acima
estão representados
pelos pontos no gráfico y versus x.
O problema aqui proposto consiste em encontrar a reta
que “melhor se
ajusta” ao conjunto de pontos deste gráfico. Um critério largamente utilizado é o de que a
melhor reta é aquela para a qual
a soma dos quadrados das distâncias verticais entre a reta e os pontos
experimentais é a menor possível.
Matematicamente, o critério dos mínimos quadrados pode ser traduzido da seguinte forma. Se yi são os valores experimentais de y correspondentes aos valores xi de x e y(xi) são os valores de y calculados pela equação da reta para cada xi, então yi - y(xi) são as diferenças entre os valores experimentais e teóricos para cada xi . Somando os quadrados destas diferenças, sobre os n pares ordenados obtém-se a função x2 que se escreve como.
Para a tabela acima, o grafico seria:
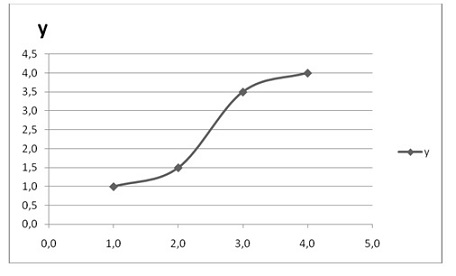
Porém, o objetivo é encontrar a equação da reta y = a + bx
Para calcula-la usamos a seguinte fórmula
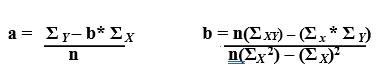
Onde, na fórmula de a = , temos :
∑Y = soma de todos os valores de Y
∑X = soma de todos os valores de X
b = é o coeficiente calculado na fórmula seguinte
n = é o número de parâmetros que estão sendo estudados, ou seja , nº de pares ordenados
Na fórmula de b = , temos :
∑XY = soma de todos os valores de X multiplicado por Y
∑X² = soma de todos os valores de X²
Os outros componentes são os mesmos definidos na fórmula do a
Para facilitar, usamos e preenchemos a tabela abaixo:

Agora é só substituir nas fórmulas:
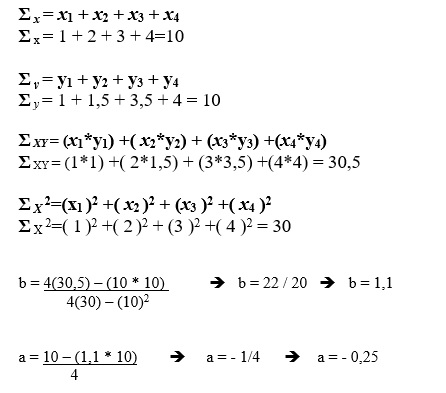
Apos calcular os valores de a e de b, substituir na equação da reta y = a + bx
Neste caso, a equação da reta é : Y = - 0,25 + 1,1 X
Substituindo os valores, a nova tabela será assim
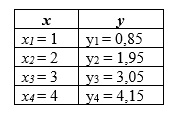
E esse será o grafico
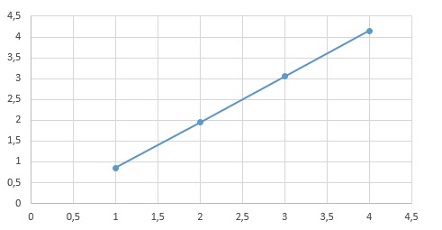
Nota-se que o gráfico agora é uma reta.
| X | Y | X*Y | X² |
|---|---|---|---|
| ∑X | ∑Y | ∑X*Y | ∑X² |
|
a = Σ y – b* Σ x n |
|||
| a =
|
|||
|
b = n(Σ xy) – (Σ x * Σ
y) n(Σ x ²) – (Σ x)² |
|||
| b =
|
|||
| Equação da reta
|
|||
|
Calcular y em função de x:
|
|||
| Digite o valor de X: | |||
| Y = | |||
|
|
|||
|
Calcular x em função de y:
|
|||
| Digite o valor de Y: | |||
| X = | |||
Histograma é um gráfico de frequência que tem por objetivo ilustrar como uma determinada amostra ou população de dados está distribuída. Ele, assim , mede quantas vezes temos determinado valor dentro dessa nossa distribuição de dados.
São várias as aplicações dos histogramas
,tais como:
- Verificar o número de produto não-conforme.
- Determinar a dispersão dos valores de medidas em peças.
- Em processos que necessitam ações corretivas.
- Para encontrar e mostrar através de gráfico o número de unidade por cada categoria.
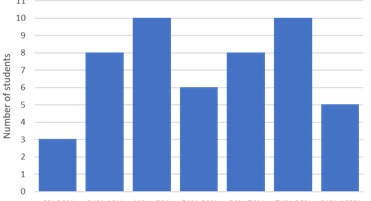
Entrando no site, clique no botao em branco, elabore a planilha,
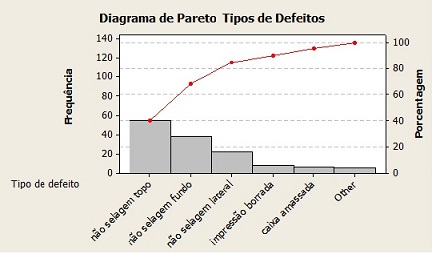
Diagrama de Pareto é um recurso gráfico utilizado para estabelecer uma ordenação nas causas de perdas que devem ser sanadas. Este esquema foi criado por um economista e sociólogo italiano, Vilfredo Pareto, que nasceu em Paris, e morreu em 1923, em Genebra. O Diagrama de Pareto tem o objetivo de compreender a relação ação - benefício, ou seja, prioriza a ação que trará o melhor resultado.
O diagrama é composto por um gráfico de barras que ordena as frequências das ocorrências em ordem decrescente, e permite a localização de problemas vitais e a eliminação de futuras perdas.
O diagrama é uma das sete ferramentas básicas da qualidade e baseia-se no princípio de que a maioria das perdas tem poucas causas, ou que poucas causas são vitais, sendo a maioria trivial.Muitas vezes, no Diagrama de Pareto são incluídos valores em porcentagem e o valor acumulado das ocorrências. A partir desta forma é possível avaliar o efeito acumulado dos itens pesquisados.
O Diagrama de Pareto é uma ferramenta muito importante porque através dele é possível identificar pequenos problemas que são críticos e causam grandes perdas.
Para o Diagrama ser aplicado, é importante seguir seis
passos básicos:
1) Determinar o objetivo do diagrama, ou seja, que tipo de
perda será investigada;
2) Definir o aspecto do tipo de perda, ou seja, como os dados
serão classificados;
3) Em uma tabela, ou folha de verificação, organizar os dados
com as categorias do aspecto
definido;
4) Fazer os cálculos de frequência e agrupar as categorias que
ocorrem com baixa frequência sob a
denominação “outros”;
5) Calcular também o total e a porcentagem de cada item sobre
o total e o acumulado;
6) Traçar o diagrama.
O Diagrama de Pareto está intrinsecamente relacionado com a
Lei de Pareto, também conhecida como
princípio 80-20, ou lei 20/80.
De acordo com esta lei, 80% das consequências decorrem de
20% das causas. Esta lei foi proposta
por Joseph M. Juran, famoso consultor de negócios, que deu esse nome como homenagem ao
economista italiano Vilfredo Pareto.
Durante as suas pesquisas, Pareto descobriu que 80% da
riqueza estava nas mãos de apenas 20% da
população.
Através desta lei é possível afirmar que:
20% dos clientes são responsáveis por mais de 80% dos lucros de uma determinada empresa;
Mais de 80% das descobertas no mundo científico resultam de 20% dos cientistas.
Fluxograma de processo é uma ferramenta que serve para representar por meio de desenhos os processos de uma empresa. Para isso, são usadas formas geométricas, setas e descrições breves. O objetivo é documentar atividades de maneira simples e fácil de repassar para os colaboradores.
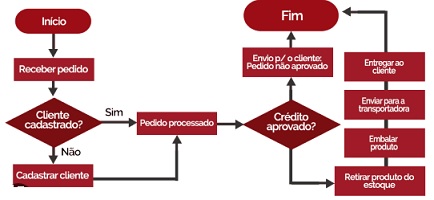
Cada passagem do fluxograma é representado por um símbolos. Cada
um deles tem um significado para cada operação.
Abaixo, os simbolos e seus significados.

Terminal:é utilizado para representar o início ou o fim de um processo ou para referir-se a outro processo que não seja objeto de estudo.

Operação: ou processo, representa qualquer ação para criar, transformar, conferir ou analisar uma operação ou procedimento. Dentro do símbolo, descreve-se o objeto da ação

Conector: indica onde contnua a seqüência do fluxo (quando não há espaço suficiente para a continuação do desenho).

Fluxo: indica o sentido do processo

Decisão: indica um ponto no processo que apresenta ações condicionantes, onde há caminhos alternativos, se acontecerem determinado evento (sim ou não / falso ou verdadeiro).

Operação manual:Este ícone simboliza que o estágio do processo deve ser efetivado de forma manual. Um exemplo prático é quando algum equipamento necessita ser desligado manualmente diariamente após o término das atividades.


Documento:representa qualquer documento ou formulário.

Espera:Em determinados momentos, entre uma fase e outra, é fundamental estabelecer um período de espera. Sempre que for preciso aguardar para avançar para outra etapa, este símbolo deverá ser utilizado.

Área/Cargo: indica o nome do cargo ou da área que executará determinada atividade

Arquivo: representa o arquivamento da documentação inerente ao processo
O Diagrama de Ishikawa (conhecido também
por Diagrama de Causa e
efeito ou Diagrama de espinha de peixe) é uma ferramenta visual para levantar todas
as possíveis causas de um problema e assim descobrir quais são as verdadeiras
causa-raízes do problema.
O diagrama é conhecido por esses três nomes porque foi
criado pelo expert em
controle de qualidade Kaoru Ishikawa na década de 60, sua forma visual se assemelha
a um esqueleto de peixe e o diagrama levanta todas as causas e efeitos do processo
para identificar a causa (ou causas) raíz do problema.
Basicamente sua equipe faz um Brainstorm (conjunto de
ideias) e levanta todos as
possíveis causas de um problema que deseja resolver. Começando pelas causas mais
diretas (ossos principais do peixe), até causas secundárias (ossos menores) que
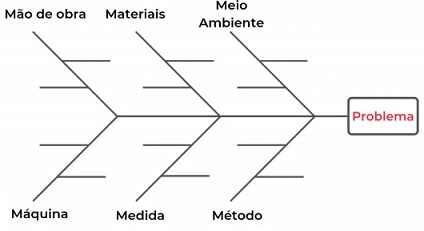
acabariam esquecidas se não fosse pela ferramenta. Abaixo está um exemplo de um
diagrama de Ishikawa:
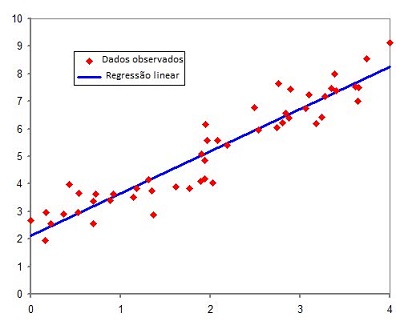
O Diagrama de Dispersão, também conhecido
como Gráfico de Dispersão, é uma das
ferramentas que compõem a qualidade.
Ele é identificado como um gráfico de eixos verticais
e horizontais,
correlacionando a causa e o efeito.
Pode-se também pode utilizar o Diagrama de
Dispersão para validar se
determinada variável independente analisada tem impacto real em determinada variável dependente.
Essa relação entre as variáveis é chamada de
correlação, e existem três
tipos: positiva, negativa e nula.
Correlação positiva: quando há uma aglomeração dos pontos em tendência crescente, significa que conforme uma variável aumenta, a outra variável também aumenta. Por exemplo, no caso da relação entre temperatura e número de sorvetes vendidos, temos uma relação positiva.
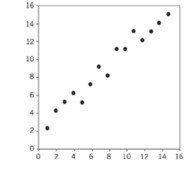
Correlação negativa: quando os pontos se concentram em uma linha que decresce, significa que conforme uma variável aumenta, a outra variável diminui, ou seja, quanto maior for a ocorrência de um dos dados, menor será a ocorrência do outro dado. Por exemplo, se correlacionarmos a taxa de natalidade com a riqueza de um país, veremos que quanto mais rico um país, menor é a taxa de natalidade.
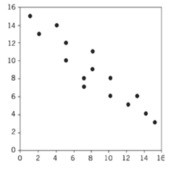
Correlação nula: quando há uma grande dispersão entre os pontos ou eles não seguem tendência positiva nem negativa, significa que não há nenhuma correlação aparente entre as variáveis.
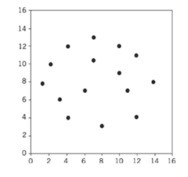
A dispersão dos pontos mostra qual a intensidade da relação: forte ou fraca.
Forte: Quanto menor for a dispersão dos pontos, maior será a correlação entre os dados.
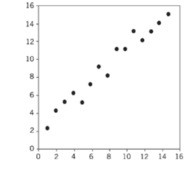
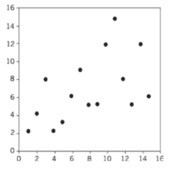
Fraca: Quanto maior for a dispersão dos pontos, menor será o grau entre os dados.
Carta de Controle , também chamada
de gráfico de controle , é um tipo de
gráfico, utilizado para o acompanhamento durante um processo. Determina uma faixa chamada de
limites de controle pela linha superior (limite superior de controle) e uma linha inferior
(limite inferior de controle) e uma linha média do processo (limite central), que foram
estatisticamente determinadas.
Realizado com amostras extraídas durante o processo,
pressupõe k uma distribuição normal
das características da qualidade. O objetivo é verificar se o processo está sob controle. Este
controle é feito através do gráfico.

Pode-se também pode utilizar o Diagrama de
Dispersão para validar se
determinada
variável independente analisada tem impacto real em determinada variável dependente.
Essa relação entre as variáveis é chamada de
correlação, e existem três
tipos: positiva, negativa e nula.
Correlação positiva: quando há uma aglomeração dos pontos em tendência crescente, significa que conforme uma variável aumenta, a outra variável também aumenta. Por exemplo, no caso da relação entre temperatura e número de sorvetes vendidos, temos uma relação positiva.

Correlação negativa: quando os pontos se concentram em uma linha que decresce, significa que conforme uma variável aumenta, a outra variável diminui, ou seja, quanto maior for a ocorrência de um dos dados, menor será a ocorrência do outro dado. Por exemplo, se correlacionarmos a taxa de natalidade com a riqueza de um país, veremos que quanto mais rico um país, menor é a taxa de natalidade.

Correlação nula: quando há uma grande dispersão entre os pontos ou eles não seguem tendência positiva nem negativa, significa que não há nenhuma correlação aparente entre as variáveis.

A dispersão dos pontos mostra qual a intensidade da relação: forte ou fraca.
Forte: Quanto menor for a dispersão dos pontos, maior será a correlação entre os dados.

Fraca: Quanto maior for a dispersão dos pontos, menor será o grau entre os dados.

A folha de verificação é aparentemente muito simples de se aplicar e por isso é considerada a mais utilizada entre as sete ferramentas da qualidade. Também conhecida como lista de verificação, checklist, ou lista de recolhimento de defeitos, é um formulário utilizado para padronizar e facilitar a coleta de dados além de uniformizar a verificação e execução de processos.
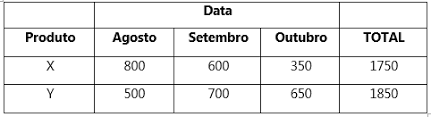
É uma formulário planejado para coletar
dados, portanto, é uma ferramenta
genérica que serve como primeiro passo no início da maioria dos controles de processo ou
esforços para solução de problemas.
Na indústria, dados registrados em folhas de verificação ajudam a entender se os produtos tem as
especificações exigidas. Por exemplo, é comum folhas de verificação para:
- Localização de defeito
- Contagem de quantidades
- Classificação de medidas
- Existência de determinadas condições
- Tipos de reclamações
- Causas de efeitos
- Causas de defeitos
Uma norma técnica (ou padrão) é um
documento, produzido por um órgão oficial acreditado para tal, que estabelece regras,
diretrizes, ou características acerca de um material, produto, processo ou serviço. A obediência
a uma norma técnica, tal como norma ISO ou ABNT, quando não referendada por uma norma jurídica,
não é obrigatória.
A precedência entre órgãos oficiais é a
mesma que há entre normas, conforme a seguinte hierarquia
- Norma internacional (ISO)
- Norma nacional
- Norma regional
- Norma organizacional
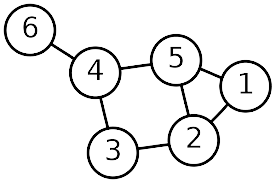
Definição de
grafo : Informalmente, um grafo pode ser visto como um conjunto de pontos,
chamado vértices, e outro de pares desses pontos, chamados arestas. Cada aresta liga um par de
pontos (extremidades) que a determina. Observe um exemplo simples de um grafo
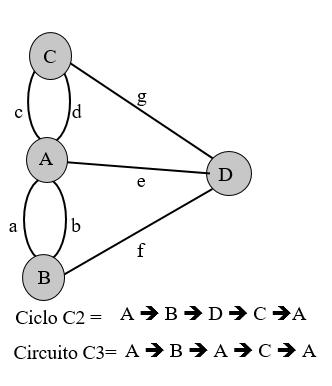
Componentes: Todo Grafo(G) é formado por Vértices(V) e Arestas(A). No Grafo de Euler temos:
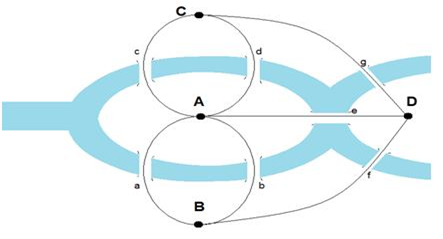
Os Vértices são os pontos e as Arestas são
os caminhos.
Repare que em Koenisberg todos os quatro vértices tem
números ímpares de arestas. Portanto, a travessia como foi sugerida é impossível
Seja o Grafo G=(V,A), temos:
Ordem - de G denotada por V, é o número de
vértices de G;
Dimensão- de G, denotada por A, é o número de
arestas de G.
Considerando o grafo G (Exemplo das pontes) tem-se: Ordem(G) = 4 vértices (A,B,C,D)
Dimensão(G) = 7 arestas (a,b,c,d,e,f,g)

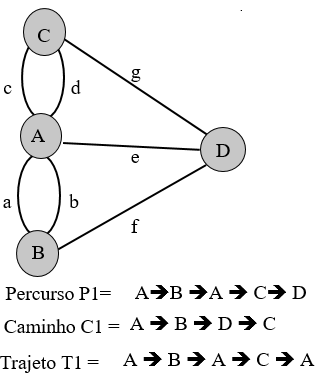
Histórico: A teoria de Grafos começou no século XVIII, na cidade medieval de Königsberg, situada no leste europeu. Esta cidade é banhada pelo rio Pregel, que a divide em quatro áreas de terra ligadas umas às outras por sete pontes, as famosas “sete pontes de Königsberg
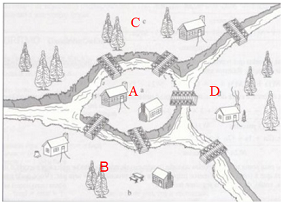
Durante muito tempo, os habitantes daquela cidade perguntavam-se se era possível cruzar as sete pontes numa caminhada contínua, sem que se passasse duas vezes por qualquer uma delas.
Leonhard Euler estudou este problema em 1736 e a partir daí, desenvolveu toda a teoria que é hoje utilizada nas mais diversas áreas que envolvem tarefas: a Teoria de Grafos Euler generalizou o problema através de um modelo de grafos
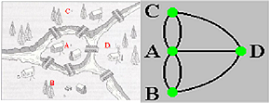
Euler descobriu que é possível atravessar um diagrama e voltar ao ponto inicial se todos os seus vértices forem pares, isto é, se cada um deles estiver ligado a um número par de arcos.
Ele também concluiu que, se houver no máximo dois vértices ímpares, também dá para atravessá-lo, mas sem regressar ao ponto de partida.
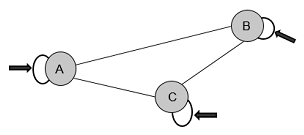
Grafo regular: Um grafo é regular quando todos os seus vértices têm o mesmo grau
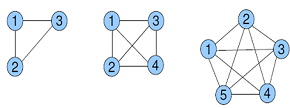
Grafo simples:
é um grafo não direcionado, sem laços e que existe no máximo uma aresta entre
quaisquer dois vértices (sem arestas paralelas).
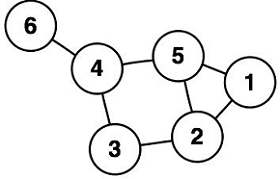
Grafo completo:É um grafo onde todos os seus vértices tem o grau máximo. Ou seja, existe aresta presente entre todos os pares de vértices.
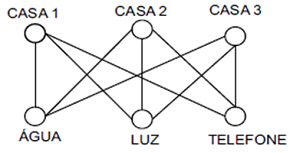
Grafo bipartido:é o grafo cujos vértices podem ser divididos em dois conjuntos, nos quais não há arestas entre vértices de um mesmo conjunto.
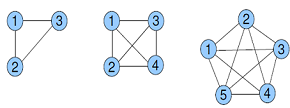
Grafo plano:é aquele que pode ser representado em um plano sem qualquer intersecção entre arestas.
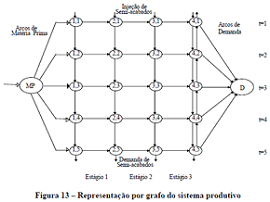
Grafo conexo: Um grafo diz-se conexo se quaisquer que sejam os vértices distintos u e v existe sempre um caminho que os une. Quando tal não acontece o grafo diz-se desconexo. A representação gráfica destes grafos contém no mínimo duas "partes" e cada uma dessas partes é uma componente conexa.
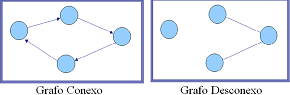
Grafo multigrafo: ou pseudografo é um grafo não dirigido que pode possuir arestas multiplas (ou paralelas), ou seja, arestas com mesmos nós finais. Assim, dois vértices podem estar conectados por mais de uma aresta.
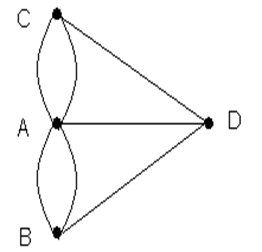
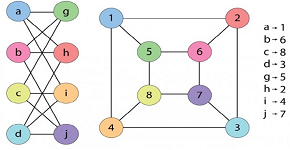
Grafos isomorfos: Dois grafos G e H são ditos Isomorfos se existe uma correspondencia 1 a 1 entre seus conjuntos de vertices que preserve as adjacencias
Grafo Euleriano: Um grafo G é dito ser Euleriano se há um ciclo em G que contenha todas as suas arestas(apenas 1 vez). Este ciclo é dito ser um ciclo Euleriano. Um grafo G é Euleriano se e somente se G é conexo e cada vértice de G tem grau par.
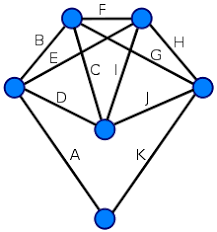
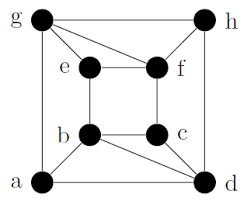
Grafo Hamiltoniano: Um grafo G é dito ser Hamiltoniano se existe um ciclo em G que contenha todos os seus vértices, sendo que cada vértice só aparece uma vez no ciclo. Este ciclo é chamado de ciclo Hamiltoniano. Sendo assim. um grafo é Hamiltoniano se ele contiver um ciclo Hamiltoniano
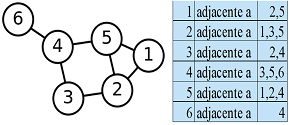
Lista de adjacencia: ou estrutura de adjacencia é a representação de todas as arestas de um grafo
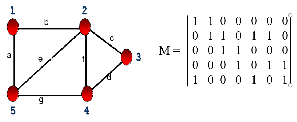
Matriz de adjacencia: é a matriz que representa as adjacencias. Usando o sistema binario, quando for adjacente , usa o numero 1 e quando nao for, o numero 0. No exemplo , a matriz fica assim:

Matriz de Incidencia: é a matriz que representa as incidencias. Usando o sistema binario, quando a aresta for incidente , usa o numero 1 e quando nao for, o numero 0
Grafo
Valorado:
também conhecidos como grafos ponderados. É quando um número real é associado aos seus vértices
e/ou às suas arestas.
Este número é frequentemente referido como o peso da ligação.
Pode representar: custos, distâncias, capacidades, .
suprimentos , demandas; tempo (trânsito, permanência, etc); confiabilidade de transmissão;
probabilidade de ocorrer falhas; capacidade de carga;
outros.
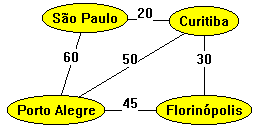
Elaboração:
Para elaborar grafos online, entrar no site https://graphonline.ru/pt/
Clicar na aba adicionar vértice
Escolhe os nomes dos vértices à direita (números, letras, customizado , etc)
Clicar na aba adicionar vértice
Depois de adicionado os vértices, clicar na aba conectar vértices e ligar um vertice a outro
As arestas podem ser direcionada ou não direcionadas.
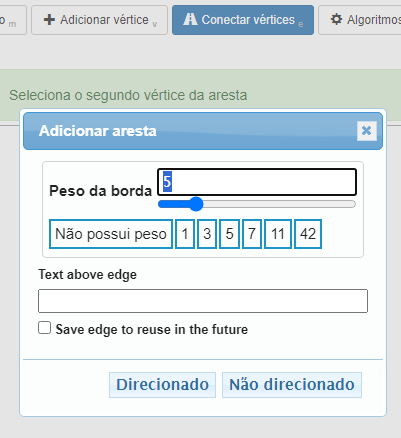
Digitar o peso (valor de cada aresta)
Dijkstra:
Edsger Wybe Dijkstra foi um importante pesquisador na área da
Ciência da Computação, mais conhecido pelo algoritmo que leva o seu nome e que calcula o caminho
mais curto entre dois vértices em um grafo.
Além disso, Dijsktra foi pioneiro em diversas setores da
computação, criando novas áreas de pesquisa e identificando e nomeando problemas novos.

O Algoritmo de Dijkstra é um dos algoritmos que calcula o caminho de custo mínimo entre
vértices de um grafo.
Escolhido um vértice como inicio da busca, este algoritmo
calcula o custo mínimo deste vértice para todos os demais vértices do grafo. Ele é bastante
simples e com um bom nível de performance.
O algoritmo de Dijkstra funciona através da construção de
uma árvore de caminho mínimo.
Ele começa com um vértice inicial e, em seguida, explora
todos os seus vizinhos, atualizando o custo para alcançar cada um deles. Em seguida,
o algoritmo seleciona o vértice com o custo mais baixo e repete o processo.
No exemplo abaixo, determinar qual o caminho mais curto do
vértice A para os demais
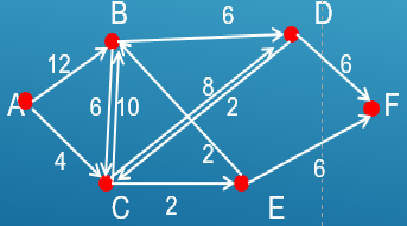
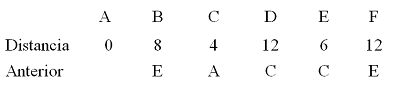
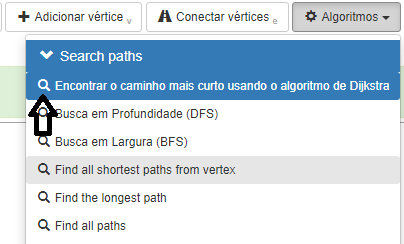
Para fazer o algoritmo de Dijkstra online , basta fazer o grafo, conforme já aprendemos, ir na aba algoritmos e escolher a primeira opção


O valor do Fluxo máximo é dado pela soma dos menores fluxos
que passa por cada aresta da rede.
Ele representa a quantidade de fluxo passando da origem ao
destino.
O problema do Fluxo Máximo é maximizar F, ou seja, transportar o maior quantidade possível de fluxo da
origem até o destino.
Esse tipo de problema pode ser usado para calcular fluxo no
trânsito, em um oleoduto, aqueduto, etc.
Para fazer o calculo online, elabore o grafo , ir em
algoritmos, desce ate encontrar fluxo máximo.
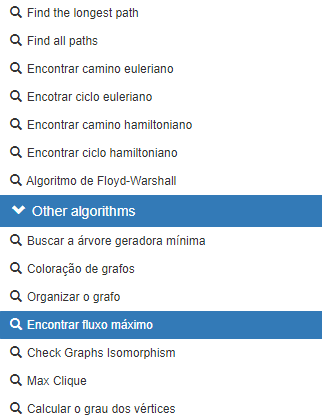
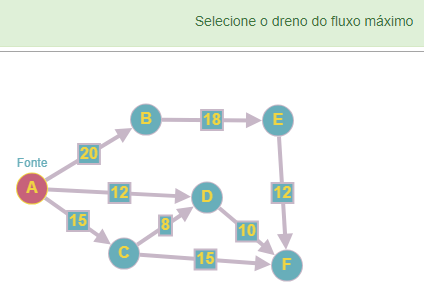
Depois selecionar o destino (dreno)
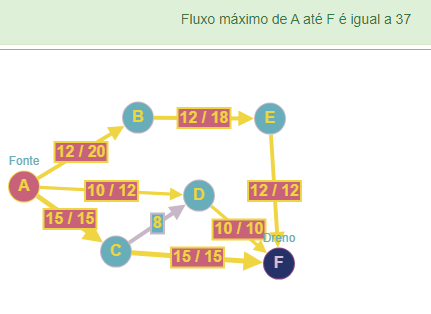
Depois selecionar o destino (dreno)
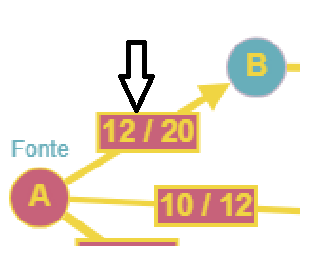
O primeiro numero na aresta corresponde à quanto passou e o
segundo, a capacidade
A aresta que liga os vértices A e B tem capacidade = 20 e no
final o fluxo que passou pela mesma foi 12
Uma das técnicas mais utilizadas na abordagem de problemas, em Métodos Quantitativos e em Pesquisa Operaciona é a programação linear.
O problema geral de programação linear é utilizado para otimizar (maximizar ou minimizar) uma função linear de variáveis, chamada de "função objetivo", sujeita a uma série de equações ou inequações lineares, chamadas restrições.
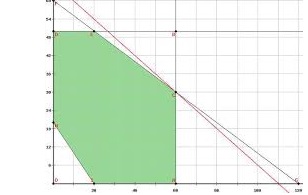
Estudaremos casos com 2 e com 3 restrições.